Ofta slänger sig personer med statistiska begrepp som de inte förstår. Nu sist var det ett facebookinlägg där en person avfärdade i en mening personlighetstestning i urvalssituationer i stil med ”det är bara att anställa de som är normala, för personlighet kan bara förklara max 9% av variationen i prestation”. Gång på gång kommer dessa argument, från PAO studenter (som hört det från sina lärare), psykologer som hört det från sin äldre kollegor och HR människor som läst någon statistik lärobok där redovisningen blandar ihop begreppen samvariation (korrelation) och kausal effekt (R i kvadrat). Så låt oss nu reda ut detta och ta nästa seriösa steg och resonera vad som funkar och inte funkar avseende bedömningstjänster.
Ofta slänger sig personer med statistiska begrepp som de inte förstår. Nu sist var det ett facebookinlägg där en person avfärdade i en mening personlighetstestning i urvalssituationer i stil med ”det är bara att anställa de som är normala, för personlighet kan bara förklara max 9% av variationen i prestation”. Gång på gång kommer dessa argument, från PAO studenter (som hört det från sina lärare), psykologer som hört det från sin äldre kollegor och HR människor som läst någon statistik lärobok där redovisningen blandar ihop begreppen samvariation (korrelation) och kausal effekt (R i kvadrat). Så låt oss nu reda ut detta och ta nästa seriösa steg och resonera vad som funkar och inte funkar avseende bedömningstjänster.
När det kommer utsagor som ”att det ändå bara förklarar 9% av variationen” kan detta härledas till en statistikbok eller lärare som beskriver determinationskoefficienten (R kvadrat). R kvadrat får man när tar korrelationen (som oftast används som effektmått i urval) och kvadrerar denna. Så om jag säger att personlighet ungefär har en korrelation på 0.30 med arbetsprestation (om man mekaniskt väger ihop big five faktorerna), då är argumentet att det förklarar ändå bara 9% av arbetsprestationen (0.30*0.30=0.09 och för att få det i % multiplicerar man 0.09 med 100=9%).
Men vad betyder egentligen 9% i detta fall. Jo det betyder att det finns ett kausalt samband mellan vad vi mäter (i detta exempel personlighet) och arbetsprestation. Dvs att det råder inget tvivel om att varje poäng på ett personlighetstest har en direkt inverkan hur jag presterar, vilket naturligtvis är orimligt att föreställa sig. Det är en mängd andra saker som påverkar om jag presterar, tex om jag är sjuk den dagen, eller om jag fått helt nya arbetstuppgifter (jag tror ni förstår vad jag menar). Detta förutsätter att det vi mäter är direkt mätbart, det finns inga fel (bias) i varken det vi mäter och det vi ska förutsäga.
Det är därför som inte R i kvadrat används i urvalsforskningen, istället använder vi oss av korrelationen, vi kvadrerar inte korrelationen, vi håller oss till att korrelationen mellan personlighet och prestation är 0.30. Det betyder att 30% av varaitionen i personlighetspoängen och prestationspoängen är gemensam, men vi säger INTE att personlighetspoängen orsakar prestationen.
I själva verket har R i kvadrat ingen praktisk betydelse över huvudtaget. R i kvadrat är ett mått på anpassning av en rak linje, ett lågt värde betyder dålig statistisk anpassning, inget annat. En korrelation däremot på .30 betyder att om vi höjer en poäng med 1 Standardavvikelse (engelskans standarddeviation, SD) då höjs sannolikt prestationen med .30 SD. Så om vi sätter ett gränsvärde på 1 SD över medel kommer vi sannolikt över tid rekrytera personer som ligger över medelpresteraren med 0.30 SD (om du vill använda korrelationen för att beräkna nytta i EURO klicka här). Att istället kvadrera korrelationen .30 så att vi istället säger att den förklarade variationen i prestation är 9% kan ej användas eftersom detta är bara ett effektmått utan praktisk innebörd.
Att kvadrera korrelationen kan också underminera ett samband som förvisso är lågt (0.30) men ändå har stor betydelse. Låt oss ta ett exempel. Vi har testat 180 personer med ett personlighetstest och vill välja de med störst sannolikhet som kommer att prestera bra på arbetet. Om vi har ett test som har noll i korrelation (och således kan förklara 0% i vårt kriterie) kommer det set ut så här.
Lågt Resultat – Låg prestation 45 personer (rätt beslut)
Högt Resultat – Hög prestation 45 personer (rätt beslut)
Lågt Resultat – Hög prestation 45 personer (fel beslut)
Högt Resultat – Låg prestation 45 personer (fel beslut)
Alltså slumpen gör att vi gör lika många fel som rätt. Vi gör 90 rätt här (45+45=90) och följdaktligen 90 fel.
Men om vi har en korrelation på 0.30 kommer det se ut så här.
Lågt Resultat – Låg prestation 65 personer (rätt beslut)
Högt Resultat – Hög prestation 65 personer (rätt beslut)
Lågt Resultat – Hög prestation 35 personer (fel beslut)
Högt Resultat – Låg prestation 35 personer (fel beslut)
Istället för att vi klassificerar 90 personer rätt kommer vi nu kategorisera 135 personer rätt, inte så dåligt om man jämför med utsagan att ”personlighet kan bara förklara max 9% av variationen i prestation”.
Om vi nu höjer blicken och granskar hur ser det ut på andra områden inom psykologin. I den senaste uppdateringen av effektstyrkor inom psykologin är en ”medium effect” uttryckt i samvariation någonstans mellan .09 and .26 (Bosco, Aguinis, Singh, Field, & Pierce, 2014). Detta uttryckt i procent (r i kvadrat) blir det 1% – 7%. Så om vi nu går tillbaka till att 9% inte är så bra, får det om man sätter det i ett relativt sammanhang en helt annan tolkning, personlighetstestning kan göra en skillnad i prestation om det jämförs med annan psykologisk forskning.
Så nästa gång du hör att någon slänger sig med begreppet förklarad variation, be hen att FÖRKLARA vad detta betyder i det praktiska arbetetet med bedömningstjänster, och framför allt, fråga om hen har ett bättre förslag hur vi kan utveckla en bedömningstjänst som har en högre effekstyrka på det som du vill förutsäga. Ofta lämnar ”förklarad varians” personerna det öppet vad som ska göras istället. Eller ännu värre, argumentet att det inte går att kvantifiera urvalsbeslut och att det jag gör istället för att personlighetstesta är mycket bättre (läs min egen intervjuteknik!!!!)
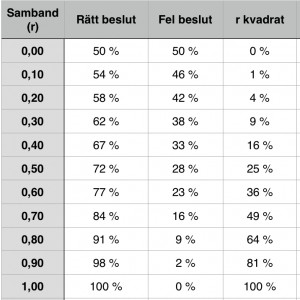
Nedan ser du en lathund om relationen mellan en korrelation och rätt och fel beslut. I den högra kolumnen jämförs rätt och fel beslut med förklarad varians (r kvadrat).
Referenser
Bosco, F. A., Aguinis, H., Singh, K., Field, J. G., & Pierce, C. A. (2014, October 13).
Correlational Effect Size Benchmarks. Journal of Applied Psychology. Advance online
publication. http://dx.doi.org/10.1037/a0038047
Ozer, D. J., (1985). Correlation and the coefficient of determination. Psychological Bulletin, 97, 307-315.